Erik Amézquita

If life gives you lemons, do directional statistics

Citrus work like lego blocks. Roughly speaking, any two citrus can hybridize and produce potentially new citrus varieties. In fact, all citrus that you see in the produce section of the market are hybrids. A grapefruit is actually a cross of a pummelo with a sweet orange. An a sweet orange is a cross of a pummelo with a sweet mandarin. And a sweet mandarin is a cross of a pummelo with a pure mandarin. A pure mandarin crossed with a pummelo can also produce a sour orange. And a sour orange crossed with a citron yields a lemon. You get the picture. Citrus are as promiscuous as it gets.

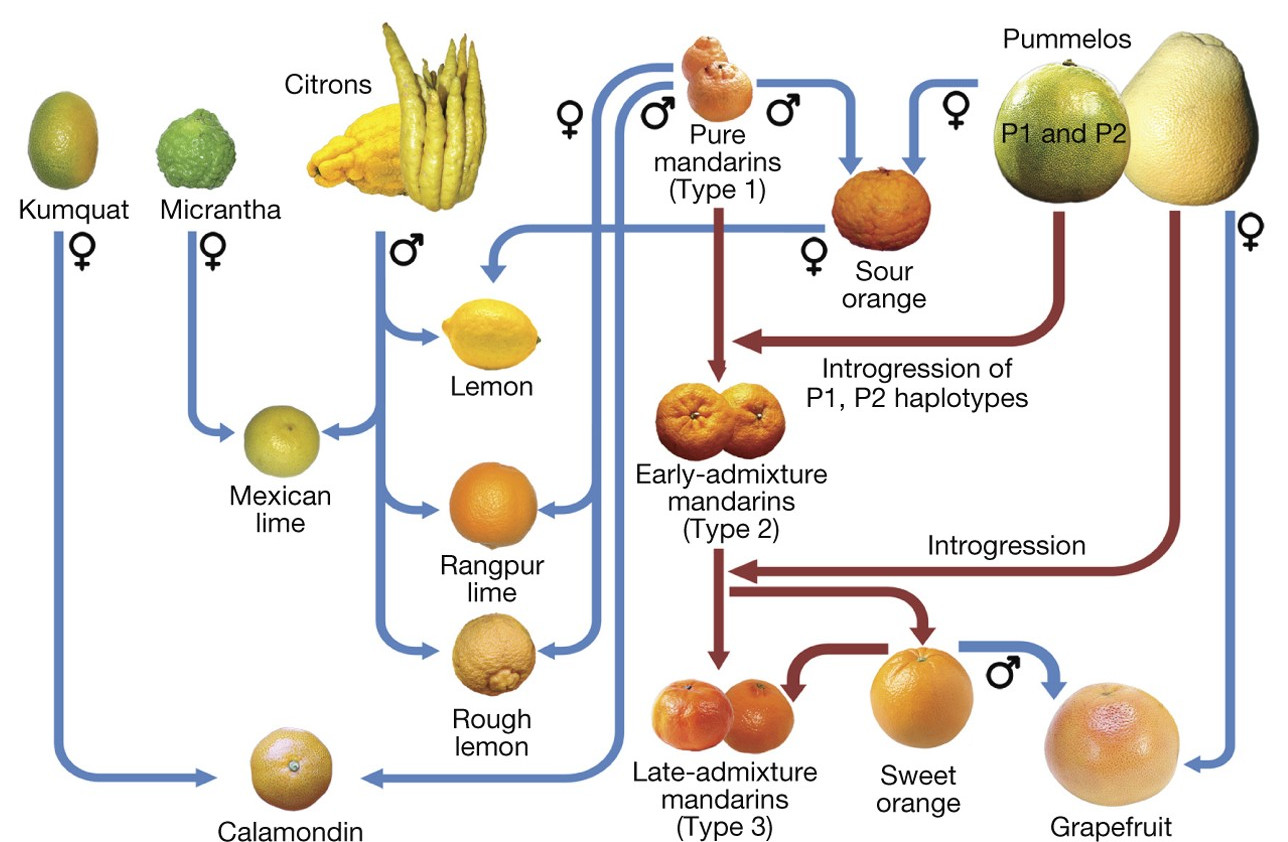
Credits: Wu et al. (2018)

This large variety of hybridization possibilities corresponds to a variety of citrus fruit shapes. Can we quantify such shape diversity? If we can mathematically describe the shape of both a pummelo and a sweet orange, would I be able to predict that their shape combination yields a grapefruit?

We are especially interested in being able to quantify and characterize the distribution of the oil glands on the citrus fruits. Citrus essential oils are important for the food and perfume industries. Oil glands also play a fundamental role in citrus fruit development. There are plenty of unknowns going forward.

The setup

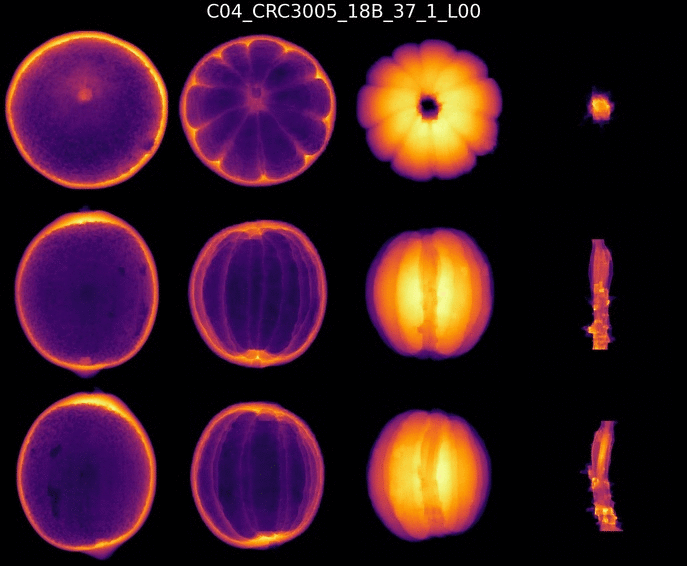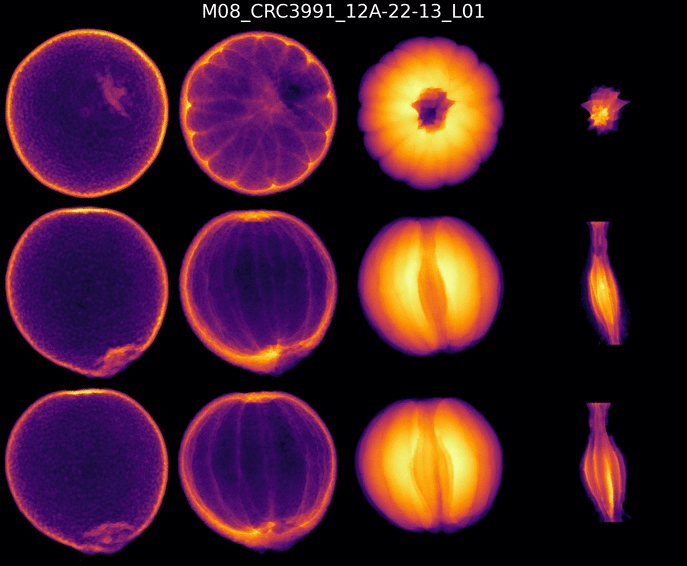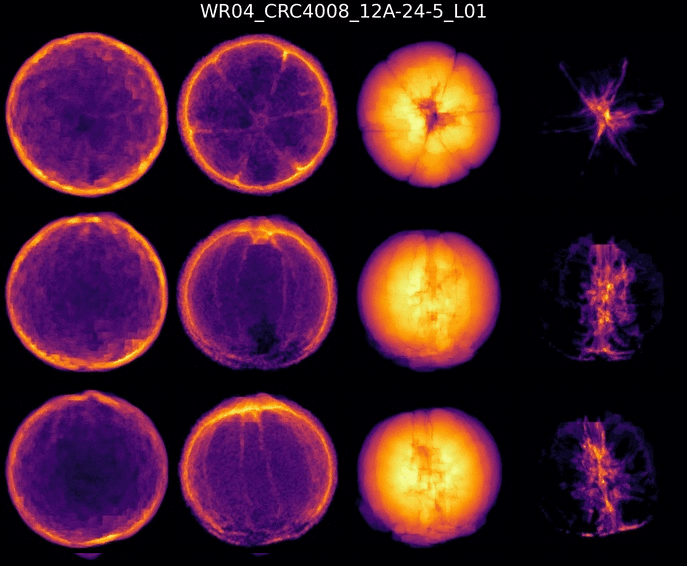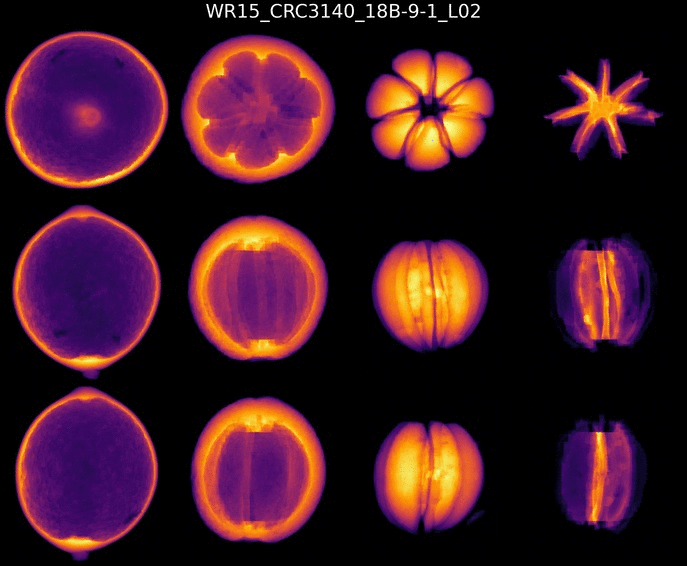
In collaboration with the Givaudan Citrus Variety Collection at University of California—Riverside, we got access to 158 individual fruit samples comprising 64 citrus varieties. These included all the fundamental citrus (citrons, pure mandarins, pummelos), close relatives (trifoliates, kumquats, microcitrus), and important hybrids (sweet oranges, lemons, etc.) These were X-ray CT scanned at Michigan State University. After a lot of image processing fiddling, we manage to segment out the central column, flesh, rind, skin, and oil glands for each citrus fruit.

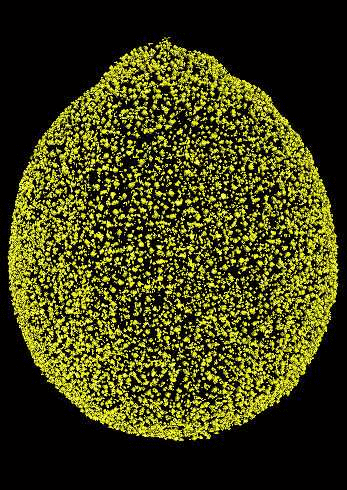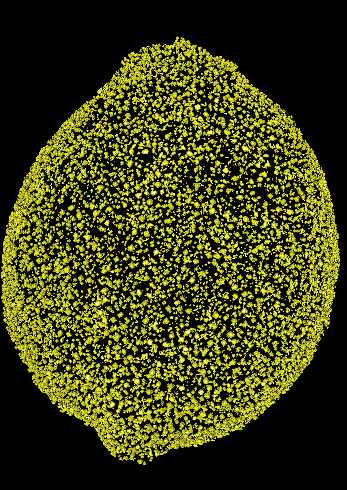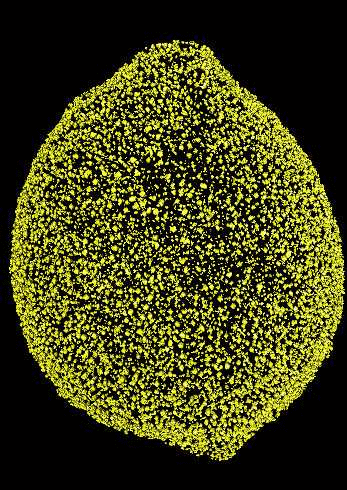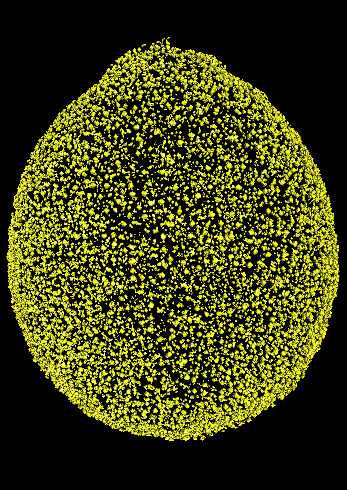
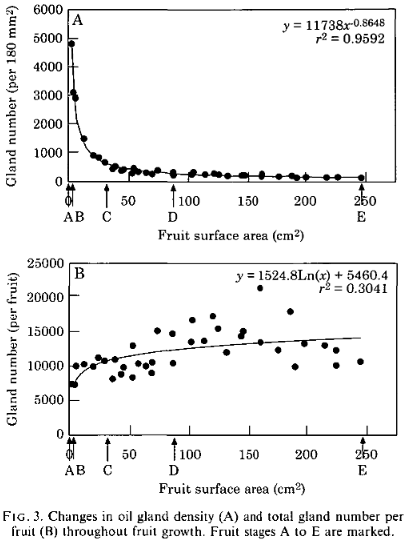
We focus on the oil glands. We can represent each oil gland as point in space where the x,y,z coordinates are the center of mass of each gland. That is, each citrus fruit now can be thought as point cloud in space (!) As a sanity check, we verify that our count of individual oil glands goes in hand with established literature.

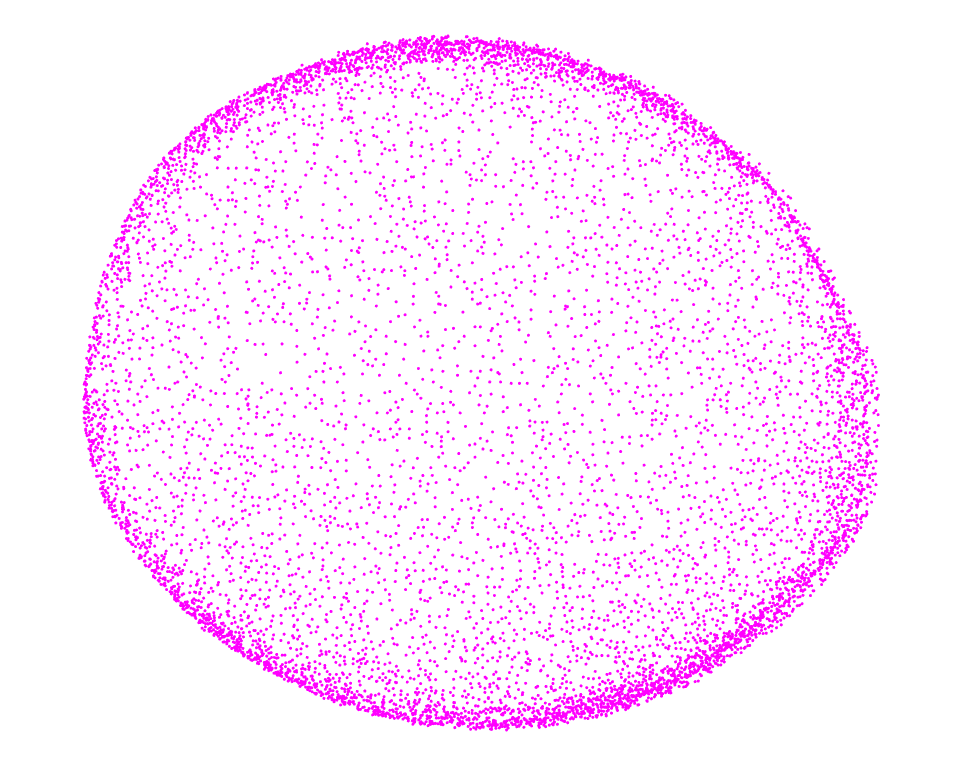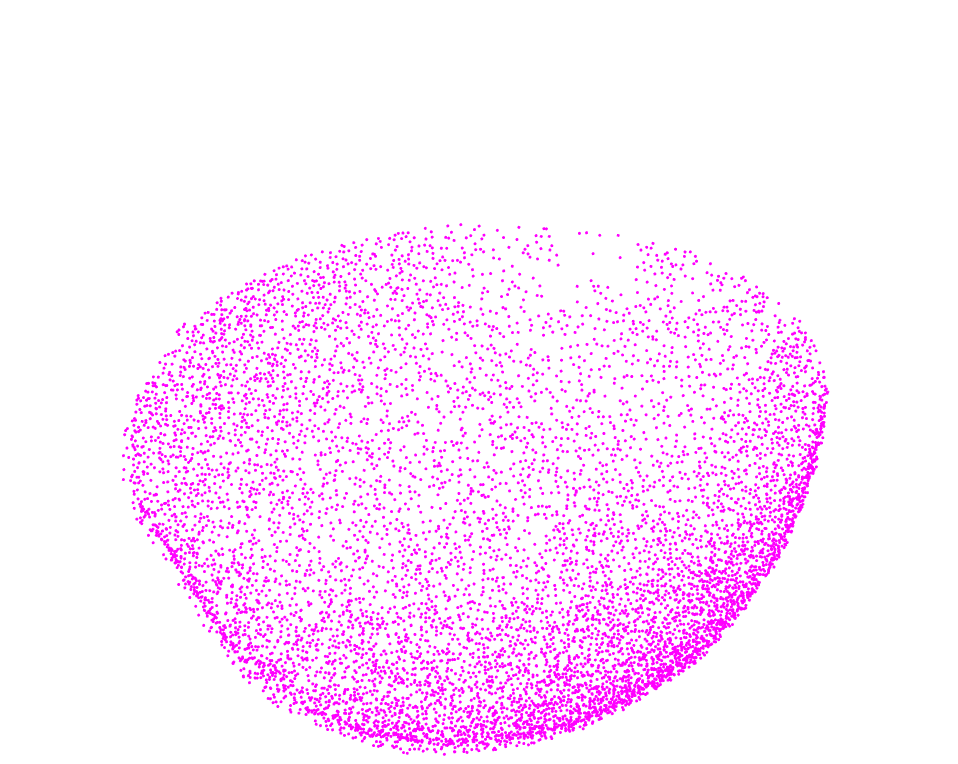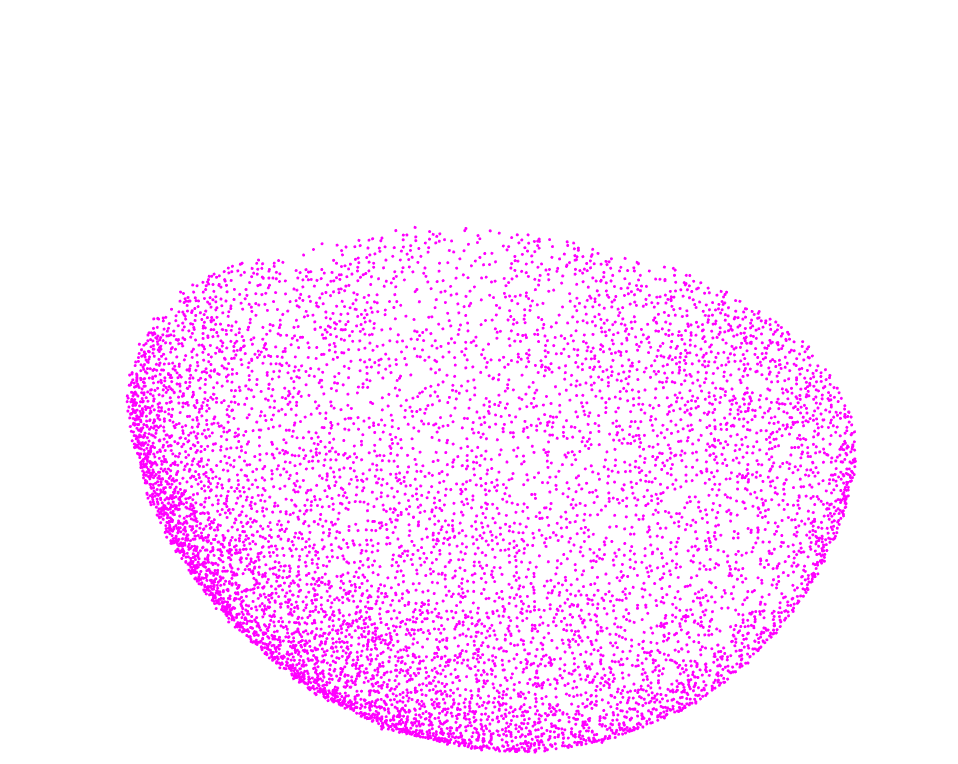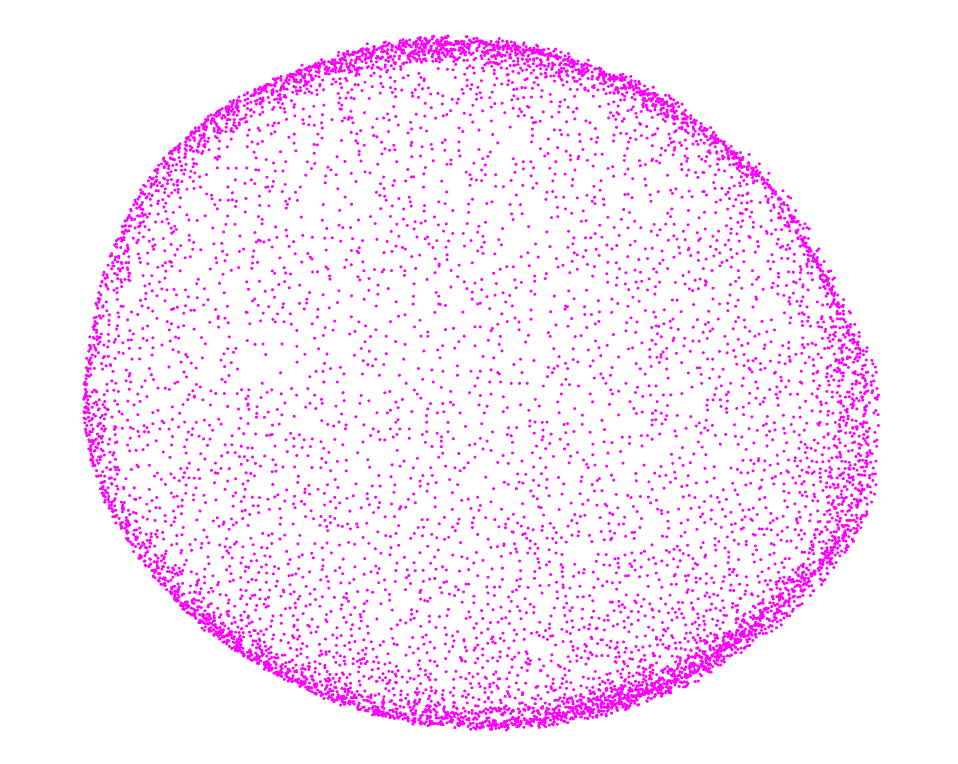
Modeling citrus fruits as ellipsoids

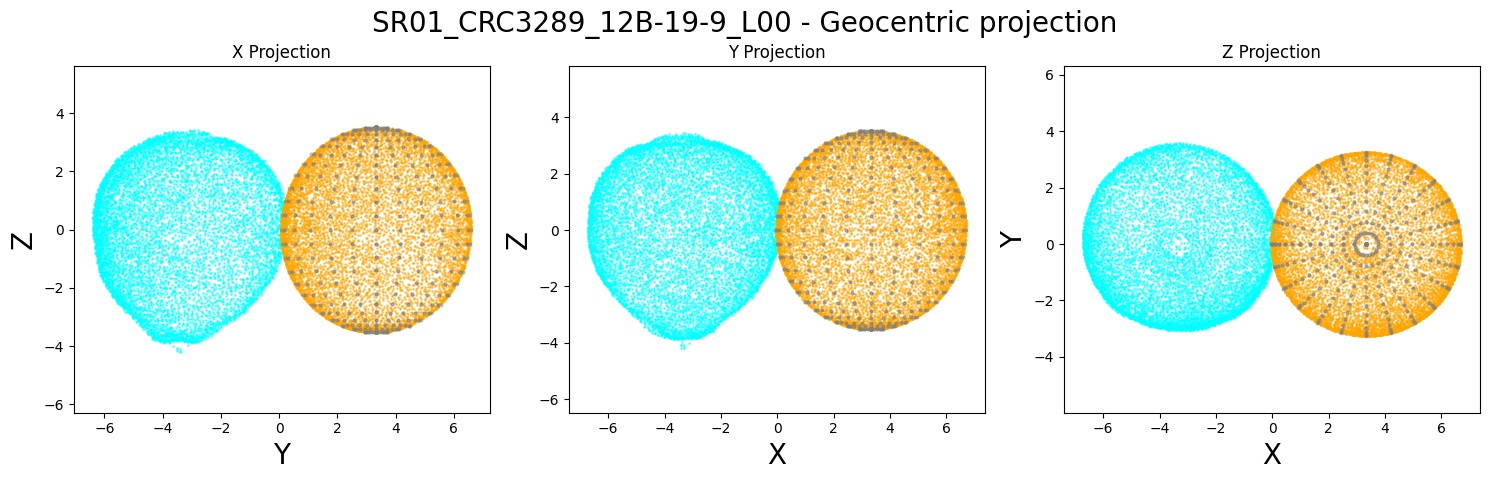
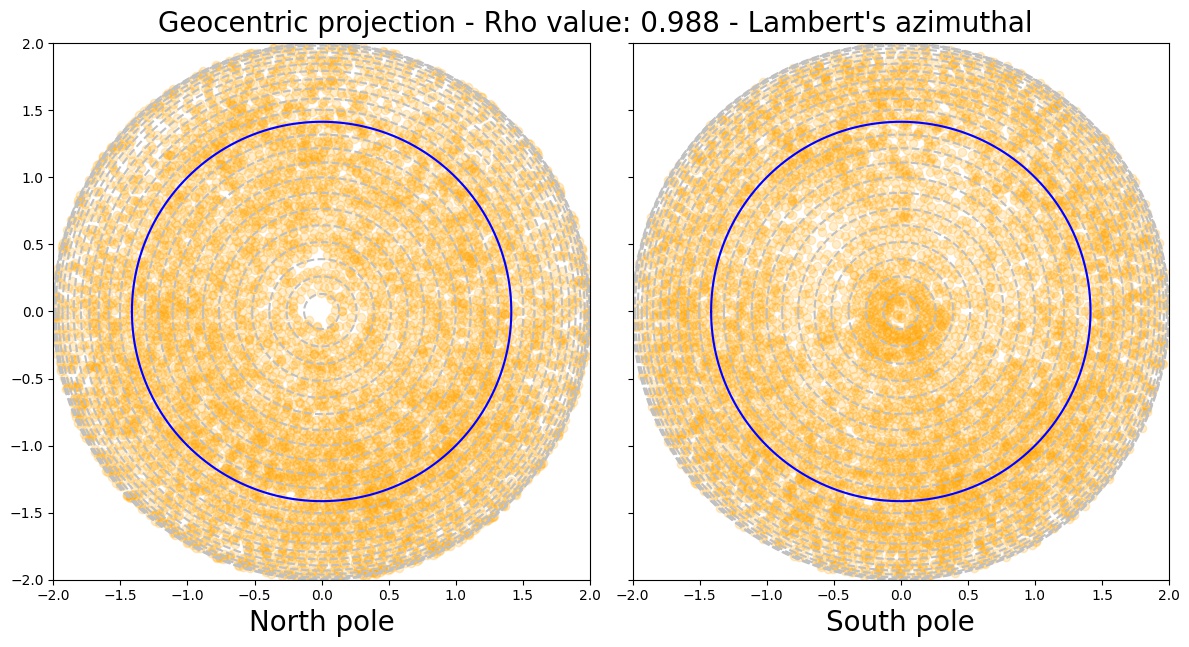
It seemed natural to model citrus as ellipsoids —an affine transformation of a sphere. This was done by simply performing ordinary least squares regression to find the best algebraic parameters of the general ellipsoid formula. Next, the point cloud made of all oil gland centers was projected to the best-fit ellipsoid. Finally, we reparameterized these centers in terms of geodetical coordinates —latitude and longitude. But latitude and longitude coordinates can be thought as lying on a unit sphere, as well. We thus have a size-independent common framework to compare all the oil glands for all the citrus fruit varieties. We visualized the oil glands on 2D via two Lambert cylindrical equal-area projections from the north and south poles.

Directional statistics

Now that all our oil gland data can be represented as points on a common unit sphere, we turn to directional statistics. Directional statistics allows us to characterize distributions specifically on circles, spheres, and related surfaces. We can also test whether a collection of points on a sphere follow a known distribution. To this end, we observed that there is no statistical evidence that supports the hypothesis of glands being uniformly distributed. Nor there was evidence in favor of rotational symmetry.

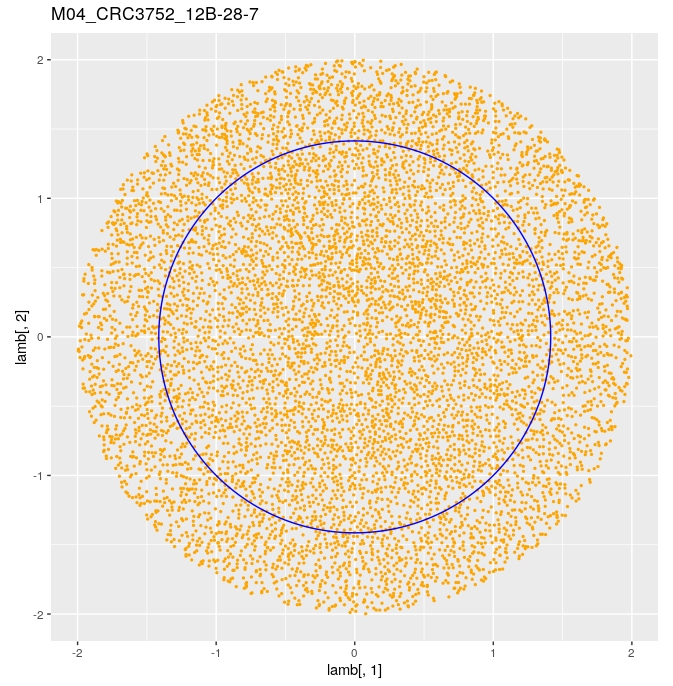
What is the distribution then?

We can compute an empiric distribution via kernel density estimation (KDE). As expected, there is a spherical-specific KDE that we can use. As in the linear case, our KDE will depend on a bandwidth parameter that will determine how smooth our empiric distribution is. We can play around with varying bandwidth parameters and observe which regions show the most dramatic distribution changes.

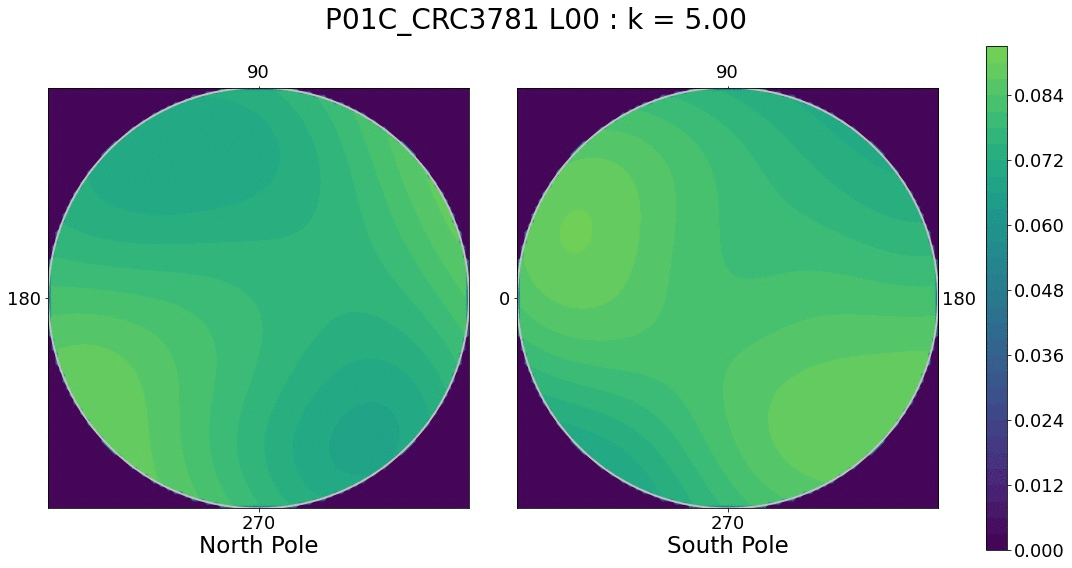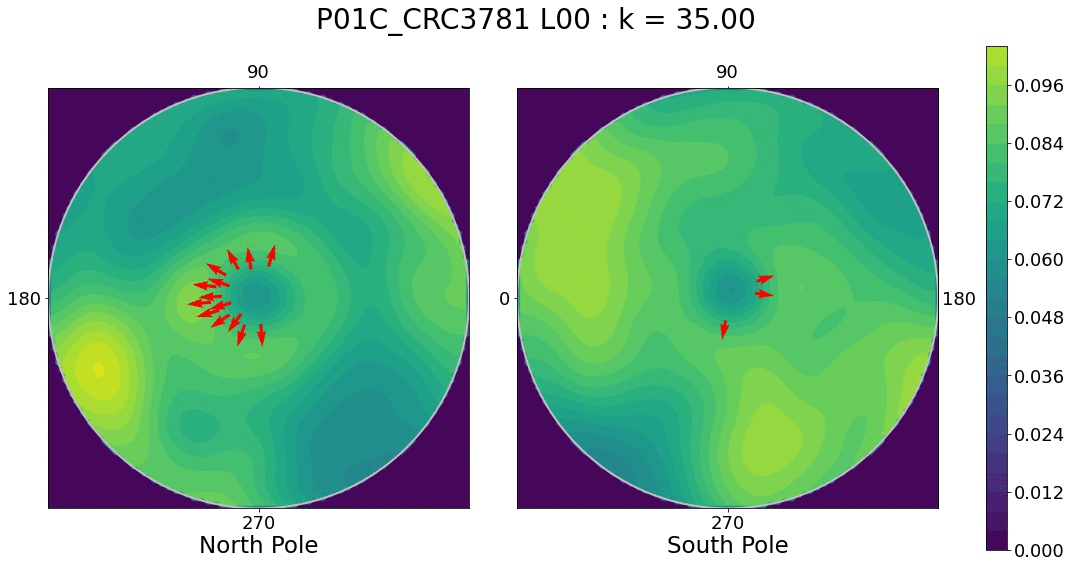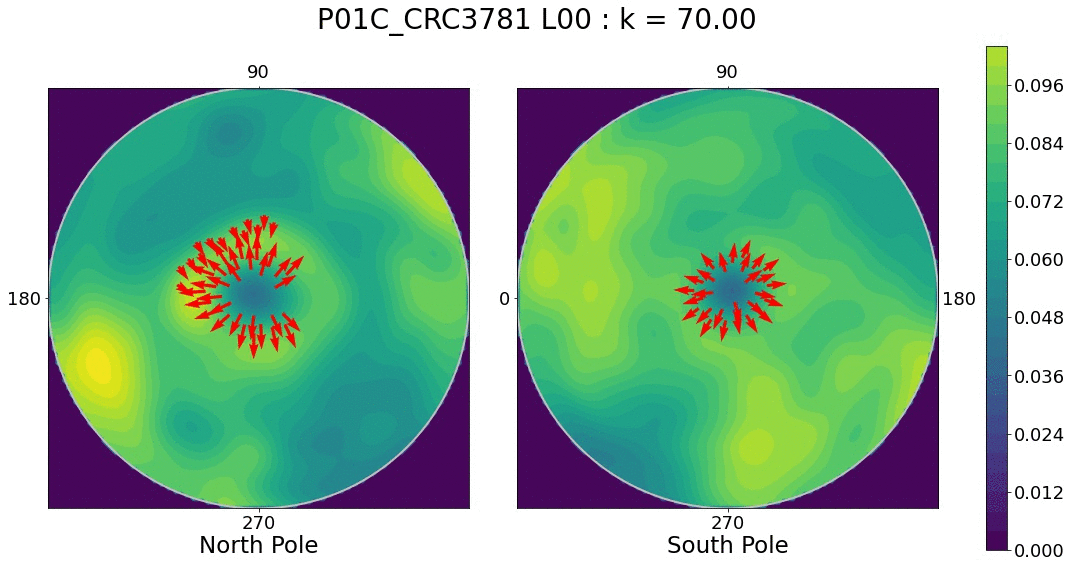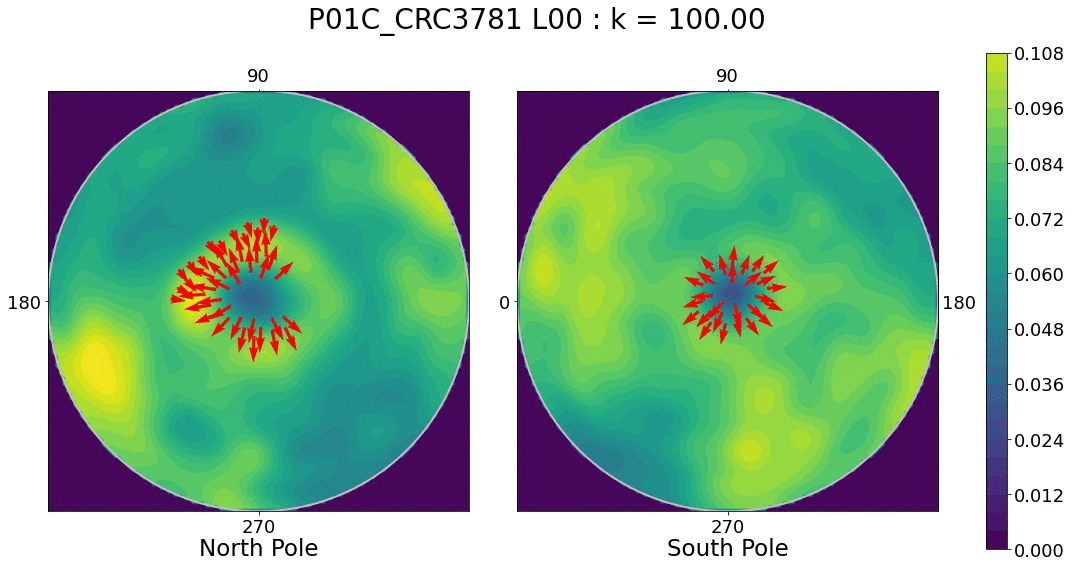
Future directions

Now that we are convinced that our pipeline enables us to quantify and compare citrus fruit shape, the potential future directions are exciting. To name a few:

Stay tuned for updates!

¡Published article: Amézquita et al. (2022)!

DOI: 10.1002/ppp3.10333

—

As slides: Presented at CMSE Brown Bag Seminar. October 2022.

As a static poster: Presented at OSUPSS. April 2022.

As a dynamic poster: Presented at OSUPSS. April 2022.

—

——————————

Go to additional resources

Other research projects

Additional Resources

Ellipsoid approximations

Given a pointcloud, a set of 3D x,y,z coordinates, what are the parameters of the best-fit ellipsoid? I was surprised there was not a straightforward, widely-accepted answer. I also realized how rusty my pre-calculus math is by now. There are a number of papers out there.

I chose Li and Griffiths (2004) as it was both mathematically and computationally the most straightforward answer I could find. They simply perform an OLS to find the algebraic parameters that minimize the algebraic residuals for the general quadric surface. In principle, this approach could produce parameters that approximate the points with a paraboloid or hyperboloid instead. You must know that your point cloud indeed looks like an ellipsoid. Supposedly they use Lagrange multipliers to guarantee that you'll always get ellipsoid paramters, but I personally did not verify it.

Credits: Li and Griffiths (2004)

This approach will give you algebraic parameters of the general quadric surface equation. To translate these into more intuitive geometric parameters (semiaxes lengths, origin, rotation, etc.), you can follow Section 2.4 of Panou et al (2020).

Ellipsoid coordinates

Credits: Diaz-Toca et al. (2020)

Once we have the ellipsoid parameters, we have to project our original point cloud onto such ellipsoid. This projection can be either:

The former projection can be computed immediately. The latter requires a much more ellaborate computation. Diaz-Toca et al. (2020) Is a very well-written breakdown of the computations needed, and they even provide a link to C code that works out of the box.

Regardless of the projection used, we can then reparameterize the original point cloud in (latitude, longitude, height) coordinates. We can then translate the (latitude, longitude) coordinates to a unit sphere. These unit sphere will be the common ground that will allow us to compare all citrus at once.

Directional statistics

Directional statistics is a relatively new branch of statistics which focuses on statistics where the domain is not a Euclidean space —as with regular statististics— but a circle, sphere, torical or cylindrical.

The 1999 seminal textbook Directional Statistics by Mardia and Jupp is pretty good. It is seminal for a reason. It basically compiles everything that was known on the subject until that point. The textbook is quite comprehensive, the index is very fleshed out, and most of the chapters are self-contained. You can jump straight into the the relevant content for the application you have in mind. It also comes with plenty of citations so you can dive deeper into the relevant literature.

More than 20 years later, Mardia and Jupp are still relevant. Their textbook is still one of the best ways to get familiar with the foundational ideas. Naturally the discipline has grown, and there have been plenty of advances since 1999. Ley and Verdebout's Modern Directional Statistics (2017) aims to be an update. They still provide some basic definitions and concepts, albeit very succintly and refer the reader back to Mardia and Jupp plenty of times. Ley and Verdebout are still a pretty good reference to know where to start the google scholar search on how to do a particular task in directional statistics. Applications are fleshed out in their complement Applied Directional Statistics.

A brief review, update, and historical overview of the discipline is provided by Pewsey and García Portugués (2021). Their last section covers on some of the available software to do actual computations. Fortunately, most of the software comes as R packages, works out of the box, and it is easy to use.

Citrus are intrinsically linked to human history

I love the Gastropod podcast. The food that we consume is more than just food. It is also a reflection of human culture and history. Food shaped our society. Citrus are no exception. As Cynthia Graber and Nicola Twilley say, «not only were these [citrus] fruits so precious that they inspired both museums and the Mafia, they are also under attack by an incurable immune disease that is decimating citrus harvests around the world.» Listen to their whole citrus episode!

Also, I highly recommend you following and watching @WeirdExplorer YouTube channel for a foodie insight into the wide, global fruit variety. He has a number of citrus-specific episodes. In particular, one of his first episodes roughly explains how most citrus are hybrids.

And this one is pretty good as well. It also contains an important message that fruit naming matters. There is a reason why the Makrut lime should be always called Makrut lime and not something else.

Citrus are quite fascinating. Their history is intrinsically linked to ours. To name a few fun facts.